Maths

National Curriculum Statement

Purpose of study
Mathematics is a creative and highly inter-connected discipline that has been developed over centuries, providing the solution to some of history’s most intriguing problems. It is essential to everyday life, critical to science, technology and engineering, and necessary for financial literacy and most forms of employment. A high-quality mathematics education therefore provides a foundation for understanding the world, the ability to reason mathematically, an appreciation of the beauty and power of mathematics, and a sense of enjoyment and curiosity about the subject.

• Aims
  The national curriculum for mathematics aims to ensure that all pupils:
  **become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop
  conceptual understanding and the ability to recall and apply knowledge rapidly and accurately.
• ** reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language
  ** can solve problems by applying their mathematics to a variety of routine and nonroutine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.

Mathematics is an interconnected subject in which pupils need to be able to move fluently between representations of mathematical ideas. The programmes of study are, by necessity, organised into apparently distinct domains, but pupils should make rich connections across mathematical ideas to develop fluency, mathematical reasoning and
competence in solving increasingly sophisticated problems. They should also apply their mathematical knowledge to science and other subjects.

The expectation is that the majority of pupils will move through the programmes of study at broadly the same pace. However, decisions about when to progress should always be based on the security of pupils’ understanding and their readiness to progress to the next stage. Pupils who grasp concepts rapidly should be challenged through being offered rich and sophisticated problems before any acceleration through new content. Those who are not sufficiently fluent with earlier material should consolidate their understanding, including through additional practice, before moving on.

Information and communication technology (ICT)
Calculators should not be used as a substitute for good written and mental arithmetic.
They should therefore only be introduced near the end of key stage 2 to support pupils’ conceptual understanding and exploration of more complex number problems, if written and mental arithmetic are secure. In both primary and secondary schools, teachers should use their judgement about when ICT tools should be used.

Spoken language
The national curriculum for mathematics reflects the importance of spoken language in pupils’ development across the whole curriculum – cognitively, socially and linguistically.
The quality and variety of language that pupils hear and speak are key factors in developing their mathematical vocabulary and presenting a mathematical justification, argument or proof. They must be assisted in making their thinking clear to themselves as well as others and teachers should ensure that pupils build secure foundations by using discussion to probe and remedy their misconceptions.

School curriculum
The programmes of study for mathematics are set out year-by-year for key stages 1 and 2. Schools are, however, only required to teach the relevant programme of study by the end of the key stage. Within each key stage, schools therefore have the flexibility to introduce content earlier or later than set out in the programme of study. In addition, schools can introduce key stage content during an earlier key stage, if appropriate. All schools are also required to set out their school curriculum for mathematics on a year-by-year basis and make this information available online.

Attainment targets
By the end of each key stage, pupils are expected to know, apply and understand the matters, skills and processes specified in the relevant programme of study.

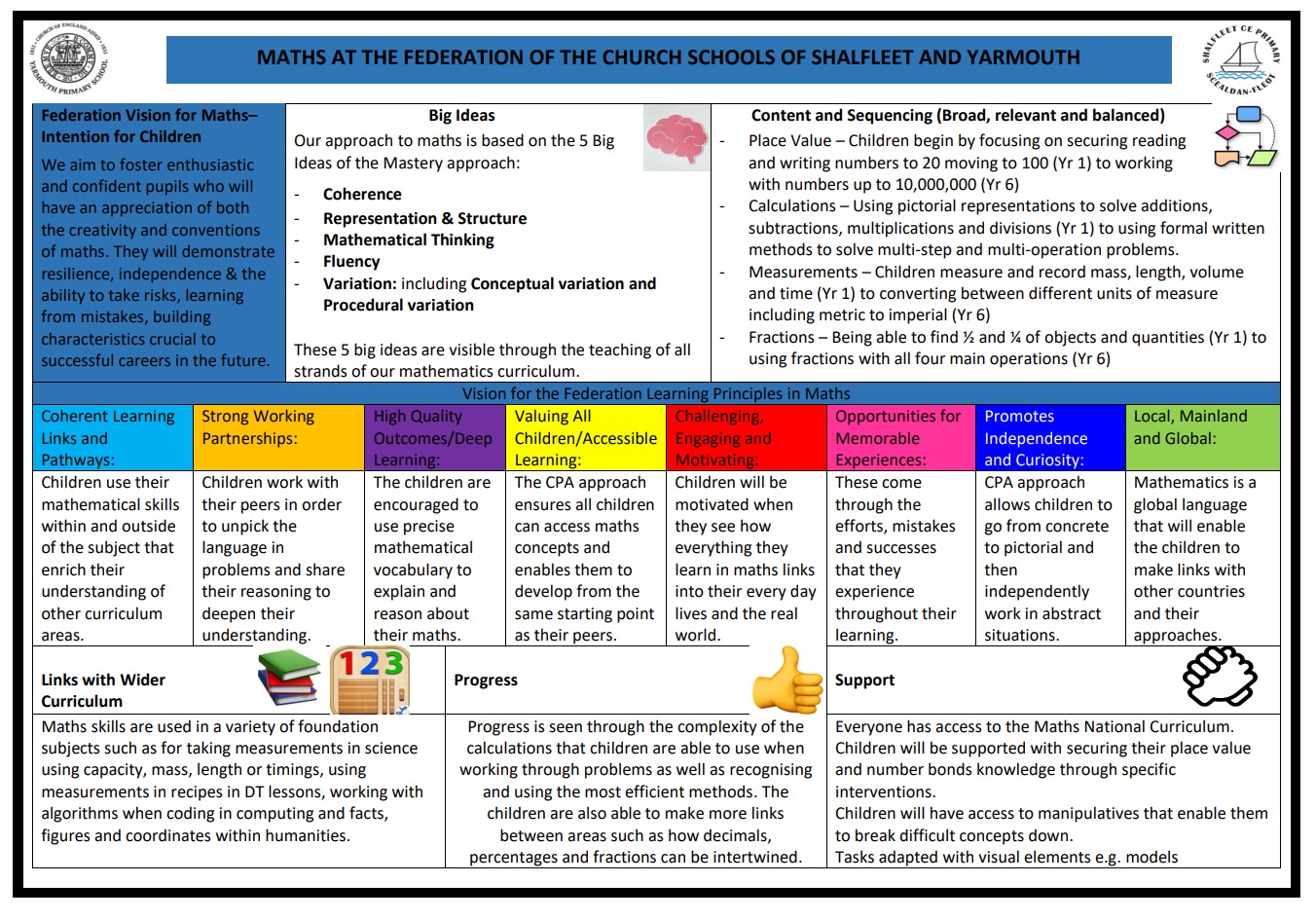
Our Intent

We aim to foster enthusiastic and confident pupils who will have an appreciation of both the creativity and conventions of maths and who demonstrate resilience, independence and the ability to take risks and learn from their and others’ mistakes.

At the Federation of Yarmouth and Shalfleet, we have adopted a CPA/Mastery approach to the teaching of maths across the school. The features of this approach is secure in some classes and in its infancy in others. This is based upon the aims of the National Curriculum for Mathematics:
‘The expectation is that the majority of pupils will move through the programmes of study at broadly the same pace. However, decisions about when to progress should always be based on the security of pupils’ understanding and their readiness to progress to the next stage. Pupils who grasp concepts rapidly should be challenged through being offered rich and sophisticated problems before any acceleration through new content. Those who are not sufficiently fluent with earlier material should consolidate their understanding, including through additional practice, before moving on.

We have high expectations of all children and promote a ‘can do’ attitude for all with an emphasis on embracing mistakes and their significance in learning – a risk free environment where children are brave learners.
– They are given a chance to believe in themselves and develop resilience and perseverance when faced with mathematical challenges.
– They regularly revisit content – retrieval practice- to recall prior knowledge.
– Mental fluency is developed through regular practice to enable rapid recall and thus allow connections and links to be made and patterns spotted. This will support conceptual understanding and procedural fluency.
– Mathematical reasoning is developed through investigations with children conjecturing about their maths.
– Children will be taught how to read, write and talk like a mathematician – in both written and verbal explanations, using stem sentences to help with an emphasis on the use of precise mathematical vocabulary.
– Children are given the opportunity to notice patterns and then to generalise.
– Mathematical concepts are set in the context of real life and children apply their maths to a range of different types of problems.
– They will be given the opportunity to apply their mathematical knowledge to other subjects.

Implementation

At Shalfleet and Yarmouth CE Primaries, our mastery approach to the curriculum is designed to develop children’s knowledge and understanding of mathematical concepts from Early Years to the end of Year 6. It uses the Concrete, Pictorial and Abstract (CPA) approach.

• We follow the National Curriculum and use White Rose Maths Hub Schemes of Work (blocked practice) for planning and assessment.
• Planning is supported by the NCETM PD materials – the Spines –Maths No Problem text books and our calculation policy to ensure a consistency of representations and models of the CPA approach.
• Teachers are clear in what children need to know and do and understand ‘where their children need to be’ through a secure understanding of year group expectations and/or pre key stage expectations and ongoing formative assessment.
• Teachers know how they are going to progress children through the use of a range of strategies, representations & manipulatives that promote independence, mastery and high expectations of ALL.
• Lesson structure incorporates the CPA approach so that children are taught through clear modelling and have the opportunity to develop their knowledge and understanding of mathematical concepts using concrete resources and moving to pictures, words and numbers.
• Adults are effectively deployed, specifically during introductions/plenaries & keep-up sessions.
• At the start of each unit, key vocabulary is introduced and revisited regularly to develop language acquisition, embedding as the unit progresses.
• There is dedicated time for mental fluency – using counting sticks, Number Sense and Times Tables Rock Stars as appropriate.
• Concepts previously learnt are revisited and recapped regularly, giving children opportunities to make connections across maths and the wider curriculum. They have the opportunity to link new learning to prior learning, allowing for a deeper understanding.
• Children with additional needs are included in whole class lessons and teachers provide scaffolding and relevant support as necessary. For those children who are working outside of the year group curriculum, individual learning activities are provided to enable progression.
• Reasoning and problem solving are integral to the activities that children are given to develop their mathematical thinking.
• Maths is incorporated across the wider curriculum.
• Children who have shown their understanding at a deep level within the unit, will have opportunities to apply these skills at a greater depth in a range of ways.
• Feedback is given in line with the feedback policy. Formative assessment/AFL within the lesson will inform teachers of the children who are in need of support or challenge.
• In order to support teacher judgements, children will be assessed using appropriate year group related White Rose End of Block and End of Term assessments and EYFS, Y2, Y6 standardisation. Gap analyses undertaken will inform planning.
• Lesson drop-ins undertaken to: ask children about their learning (in pupil conferences); look at books to see the use of mathematical representations and precise language in children’s work and to confirm that a coherent learning journey – incorporating the small steps – is evident.
• The maths lead works with SLT to analyse key data and provide feedback where needed to inform on progress and future actions.
• Moderation undertaken – in-house, across-schools, Local Authority events.

Why do we use the block practice of NCETM/White Rose?  The blocked approach to teaching and learning allows children to overlearn so that depth of understanding can be achieved and we are then able to build on these secure foundations of knowledge when making connections with other concepts.  We aim to incorporate spaced practice which enables recapping and revisiting concepts and learning before it’s forgotten.

For more information you can go to https://whiterosemaths.com/  where you can also find resources specifically for parents.